An analysis of MLB umpire strike zones in 2023

Authors: Matthew Schneider and Karim Elsharkawy

This project analyzes the behavior of umpires in Major League Baseball (MLB) in 2023. Baseball is one of the most important sports in the United States, with its origins tracing back to the 1840s, although the modern game did not appear until the 1920s with the "live-ball era." The game involves two teams who take turn batting and fielding the ball. When a team is fielding the ball, a player known as the pitcher must throw a ball to a batter who tries to hit it with a bat. The goal is to hit the ball into the field of play and run the bases before he can be put out. Baseball is officiated by umpires. At the Major League level, there are usually four umpires per game, one per base. One umpire is assigned to home plate. This home plate umpire has the additional responsibility of managing what is known as the strike zone.

A batter only has a limited number of opportunities to swing at pitches during one plate appearance, or the time he is at bat against a pitcher. The pitcher is also expected to throw pitches that can be reasonably expected to be hit by a batter. These aspects of the game are mediated through something called the count, which measures the number of balls and strikes. When the pitcher throws a ball to the batter, the batter may choose to swing or not to swing. If the batter does not swing at the pitch (said to be a taken pitch), then the umpire must judge whether the path of the ball crossed through the strike zone.

• If the umpire deems that the ball crossed through the strike zone, then a strike is added to the count.
• If the umpire deems that the ball did not cross through the strike zone, then a ball is added to the count.

The count can determine the result of the plate apperance: if the count reaches three strikes, then the batter is out and does not get to play anymore (this is advantageous to the fielding team, because three outs ends the inning). If the count reaches four balls, then the batter is awarded a walk and may proceed to first base for free (this is advantageous to the hitting team).

In MLB, it is the sole responsibility of the home plate umpire to make this judgement call with his eyes. As such, he may be fallible to making an incorrect call. Missed calls can have a great effect on a single plate appearance. For example, if a ball is mistakenly called a strike on a 1-1 count (1 ball, 1 strike), the count moves to 1-2 (significantly in favor of the pitcher, since the batter is one strike from striking out) instead of 2-1 (in favor of the batter). In close games, the outcome of a single pitch can affect who wins and who loses as seen in a 2022 game:

The human definition of the strike zone

According to MLB,

The official strike zone is the area over home plate from the midpoint between a batter's shoulders and the top of the uniform pants -- when the batter is in his stance and prepared to swing at a pitched ball -- and a point just below the kneecap. In order to get a strike call, part of the ball must cross over part of home plate while in the aforementioned area.

Here is a pictoral example of the 3D strike zone:

The computer definition of the strike zone

Computer pitch trackers use a more simplified definition of the strike zone, which we will adopt for our analysis. This is consistent with MLB's own internal zone rating metrics and other public sources for strike zone analysis. Compared to the rulebook definition, which prescribes a 3D zone in the shape of home plate, the computer zone is a 2D rectangle at the front of home plate, which we can see in the example image below outlined in blue:

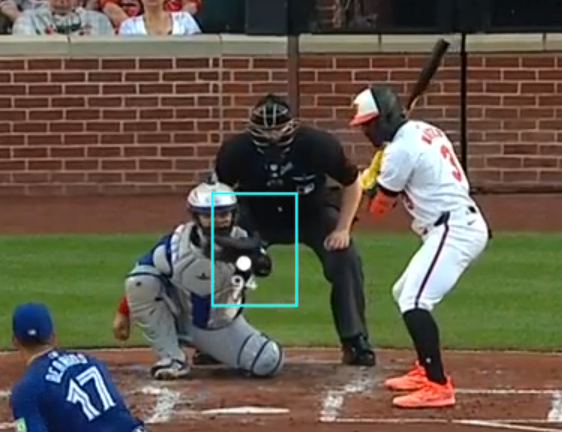
The entire baseball field is represented in three coordinate axes. The axes are represented in the dataset in units of feet. We only care about two axes, the x axis, which is the horizontal axis with respect to the image, and z axis, which is the vertical axis with respect to the picture. The reference points for the two axes are:

• x = 0 corresponds to the middle of home plate. Positive x values correspond to the left with respect to the image, negative values are to the right.
• z = 0 corresponds to the ground. Positive values of z indicate off the ground

The horizontal bounds of the strike zone correspond to the width of home plate. Home plate is 17 inches wide (or ~1.417 feet), and since x = 0 is the center of home plate, this places the horizontal boundaries of the zone at x = 0.708 and x = -0.708. The vertical bounds for the zone are dependent on the batter's stance. In the dataset, these are represented by two values, sz_top corresponding to the top bound of the strike zone, and sz_bot corresponding to the bottom bound of the strike zone.

Lastly, we need to know the position of the ball. These are encoded in the values px and pz which correspond to the position of the center the ball as it crosses the front of home plate in the horizontal and vertical direction, respectively. Together, this gives us the following labelled example:

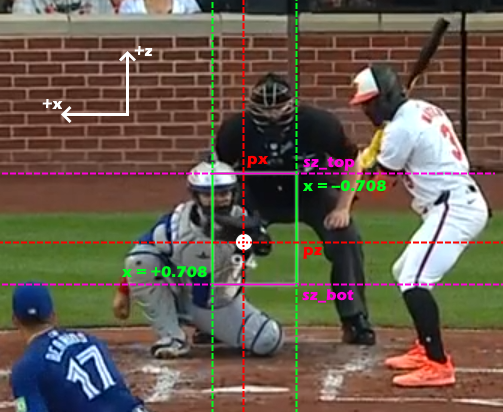
Thus, to calculate if the pitch crosses through the strike zone, we need to check any part of the ball clips through the 2D rectangle. Since the px and pz values only describe the center of the baseball, we must also consider its radius RAD, which is 0.12 feet. Thus, we must check two conditions:

• check if the pitch is horizontally in the strike zone: -0.708 - RAD <= px <= 0.708 + RAD
• check if the pitch is vertically in the strike zone: sz_bot - RAD <= pz <= sz_top + RAD

The pitch is in the strike zone, and thus should be called a strike, if and only if both of the above conditions are true. For more information and an explainer video on reading computer strike zone data, see this article.

The dataset we are using includes a column called zone, which captures the MLB Gameday zone number:

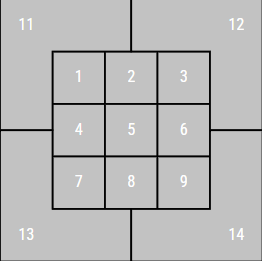
If the zone number is less than 10, then the pitch crossed through the strike zone. If the number is greater then 10, then the pitch did not cross through the strike zone. Note that 10 is not a valid number in the chart. We can rely on this data instead of doing the above calculations, although we expect both to be consistent.

First, we'll make some imports of things we need for this tutorial.

import requests
import json
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import classification_report
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
from sklearn import linear_model

pd.set_option('display.max_columns', None)

Data collection

MLB provides precise information for every pitch from every game dating back to 2015. We'll be looking at games from 2023 for this analysis.

Finding the list of 2023 games

First, we must find the list of games, which are identified by a unique ID (called game_pk) as assigned by MLB. We query MLB's StatsAPI in order to get all game_pk values from games in 2023.

r = requests.get("https://statsapi.mlb.com/api/v1/schedule",
                 params={"sportId": 1,              # indicates Major League Baseball (AL + NL)
                         "startDate": "2023-01-01", # start of 2023
                         "endDate": "2023-12-01",   # end of 2023
                         "gameTypes": "R"})         # only regular season games, no postseason or spring training

# The query includes a list of dates, and each date has a list of games for that day.
query = json.loads(r.content)

# extract each game_pk
game_pks = []
for date in query['dates']:
    for game in date['games']:
        game_pks.append(game['gamePk'])

# get rid of duplicates (happens due to postponements, which double counts the game for the originally scheduled date and actual date of the game)
games = list(set(game_pks))

print(len(games))                               # total number of games
print(games[0], games[1], games[2], games[3])   # print out first four game_pks as a sample

2430
716352 716353 716354 716355

We expect there to be 2,430 games in the regular season for 2023, based on the schedule of 162 games for 30 teams (so that 2430 = 162 * 30 / 2). Other seasons may have more or less, for example "Game 163" which used to be played as a tiebreaker in the standing, cancelled games which are not rescheduled, and, notably, the 2020 season which was shortened to 60 games per team because of COVID-19.

Getting pitch data from all 2023 games

Next, we query games from GameFinder (provided by BaseballSavant) and StatsAPI (provided by MLB) to get the pitch data from every game. The reason we need to query both sources is because the two on their own do not supply enough information for each pitch. Gamefinder reports the number of outs for a particular pitch as the number of outs following the plate appearance (rather than the number live during the at bat). StatsAPI reports the count (balls and strikes) following the pitch (not before the pitch).

Each pitch is assigned its own play_id which is consistent across BaseballSavant and StatsAPI, which allows us to easily join the DataFrames generated from the two sources together.

# This function takes in a `game_pk` and returns a DataFrame of all pitches corresponding to that game.
def get_game_pitches(game_pk):
    # download game data from gamefinder through a request
    r = requests.get("https://baseballsavant.mlb.com/gf", params={"game_pk": game_pk})
    game = json.loads(r.content)

    # collect all pitches
    # gamefinder sorts all pitch data by who is the team pitching (home/away) and has a list of all those pitches
    away_pitches = pd.DataFrame(game['team_away'])      # away team is pitching/ home team is batting
    home_pitches = pd.DataFrame(game['team_home'])      # home team is pitching/ away team is batting

    # assign top/bottom half of innings based on who is pitching
    away_pitches["half_inning"] = "bottom"
    home_pitches["half_inning"] = "top"

    # concatenate the two dataframes
    pitches = pd.concat([away_pitches, home_pitches], ignore_index = True)

    # place information about the game as a whole in each row
    pitches["away_team"]   = game["scoreboard"]["teams"]["away"]["name"]
    pitches["away_abbrev"] = game["scoreboard"]["teams"]["away"]["abbreviation"]
    pitches["home_team"]   = game["scoreboard"]["teams"]["home"]["name"]
    pitches["home_abbrev"] = game["scoreboard"]["teams"]["home"]["abbreviation"]

    pitches["date"]      = game["scoreboard"]["datetime"]["officialDate"]
    pitches["day_night"] = game["scoreboard"]["datetime"]["dayNight"]

    # we need to find who is the home plate umpire for this particular game
    # we search through the list of officials to find which one is designated "Home Plate"
    try:
        umpire = next((umpire for umpire in game['boxscore']['officials'] if umpire["officialType"] == "Home Plate"), None)["official"]["fullName"]
    except KeyError:
        umpire = None
    pitches["plate_umpire"] = umpire    # add as a new column

    pitches.drop(columns=["outs"], inplace=True)    # drop this column since it is inaccurate

    # get the remaining information through StatsAPI
    r = requests.get(f"https://statsapi.mlb.com/api/v1.1/game/{game_pk}/feed/live")
    game = json.loads(r.content)

    # this function extracts a dataframe of pitches from statsapi v1.1 data
    def get_pitches_play(play):
        df = pd.DataFrame(play['playEvents'])
        df['event_description'] = play['result']['event']
        df['event_type'] = play['result']['eventType']
        return df[df['isPitch'] == True]

    # get the pitches for all the plays
    # statsapi organizes pitches by plate appereance (i.e. a list of plate appearances, each with a list of pitches from that plate appearance)
    extra = pd.concat([get_pitches_play(play) for play in game['liveData']['plays']['allPlays']], axis=0, ignore_index = True)

    # the data is stored a dictionary of dictionaries, so we flatten all these so that all the parameters are at the same level
    extra = pd.concat([extra.drop(['count'], axis=1), extra['count'].apply(pd.Series)], axis=1)
    extra = pd.concat([extra.drop(['details'], axis=1), extra['details'].apply(pd.Series)], axis=1)
    extra = pd.concat([extra.drop(['pitchData'], axis=1), extra['pitchData'].apply(pd.Series)], axis=1)
    extra = pd.concat([extra.drop(['breaks'], axis=1), extra['breaks'].apply(pd.Series)], axis=1)

    # the `runnerGoing` column is either True or blank (NA), so we fill the NAs with false
    try:
        extra['runner_going'] = extra['runnerGoing'].fillna(False)
    except KeyError:
        extra['runner_going'] = False
    
    # set extra break information to NaN if it is not available
    if 'spinDirection' not in extra:
        extra['spinDirection'] = np.NaN
    if 'breakVertical' not in extra:
        extra['breakVertical'] = np.NaN
        extra['breakHorizontal'] = np.NaN
        extra['breakLength'] = np.NaN
        extra['breakAngle'] = np.NaN

    # rename `play_id` for easier merging
    extra.rename({"playId": "play_id"}, inplace=True, axis=1)
    # extract just the extra columns we want from statsapi
    extra = extra[['play_id', 'outs', 'runner_going', 'spinDirection', 'event_type', 'event_description',
                   'breakVertical', 'breakHorizontal', 'breakLength', 'breakAngle']]    
 
    # merge the two dataframes together    
    return pd.merge(pitches, extra, how="left", on=["play_id"])

Now that we have a function which gets us the pitches corresponding to an individual game_pk, let's run it on all the game_pks we have for 2023 and compile the results together. Expect this routine to take a lot of time!

game_pitches = list(map(get_game_pitches, games))

all_pitches = pd.concat(game_pitches, ignore_index = True)
all_pitches.set_index("play_id", inplace=True)
all_pitches.head()

C:\Users\Matthew\AppData\Local\Temp\ipykernel_68740\602634917.py:3: FutureWarning: The behavior of DataFrame concatenation with empty or all-NA entries is deprecated. In a future version, this will no longer exclude empty or all-NA columns when determining the result dtypes. To retain the old behavior, exclude the relevant entries before the concat operation.
  all_pitches = pd.concat(game_pitches, ignore_index = True)

	inning	ab_number	cap_index	batter	stand	batter_name	pitcher	p_throws	pitcher_name	team_batting	team_fielding	team_batting_id	team_fielding_id	result	des	events	contextMetrics	strikes	balls	pre_strikes	pre_balls	call	call_name	pitch_type	pitch_name	description	result_code	pitch_call	is_strike_swinging	balls_and_strikes	start_speed	end_speed	sz_top	sz_bot	extension	plateTime	zone	spin_rate	px	pz	x0	y0	z0	ax	ay	az	vx0	vy0	vz0	pfxX	pfxZ	pfxZWithGravity	pfxZWithGravityNice	pfxZDirection	pfxXWithGravity	pfxXNoAbs	pfxXDirection	breakX	breakZ	inducedBreakZ	is_bip_out	pitch_number	player_total_pitches	player_total_pitches_pitch_types	game_total_pitches	rowId	game_pk	player_name	hit_speed_round	hit_speed	hit_distance	xba	hit_angle	is_barrel	hc_x	hc_x_ft	hc_y	hc_y_ft	runnerOn1B	runnerOn2B	runnerOn3B	half_inning	away_team	away_abbrev	home_team	home_abbrev	date	day_night	plate_umpire	outs	runner_going	spinDirection	event_type	event_description	breakVertical	breakHorizontal	breakLength	breakAngle
play_id
fd40dc91-e458-47d4-81d4-bdd654781440	1	6	0	672580	R	Maikel Garcia	650633	R	Michael King	KC	NYY	118	147	Lineout	Maikel Garcia lines out to center fielder Este...	Lineout	{}	0	0	0	0	S	Strike	SI	Sinker	Called Strike	C	called_strike	False	00	92.0	85.2	3.531020	1.612927	5.922587	0.407594	7.0	2491.0	-0.292692	2.207051	-2.461166	50.003600	5.557445	-17.086921	25.264212	-25.635070	8.973728	-133.710840	-4.062951	-9.312735	3.563786	-26.040910	26.0	↓	16	-16	→	15.0	27.0	5.0	Y	1	1	1	23	23-716352	716352	NYY	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	bottom	New York Yankees	NYY	Kansas City Royals	KC	2023-10-01	day	Clint Vondrak	0	False	200.0	field_out	Lineout	-26.2	15.2	7.2	30.0
60d12f55-1c47-42da-8f3e-d3e2e6e47ee2	1	6	0	672580	R	Maikel Garcia	650633	R	Michael King	KC	NYY	118	147	Lineout	Maikel Garcia lines out to center fielder Este...	Lineout	{}	1	0	1	0	S	Strike	FF	4-Seam Fastball	Swinging Strike	S	swinging_strike	True	01	93.8	86.9	3.590000	1.730000	5.691580	0.398518	11.0	2330.0	-1.158241	3.385914	-2.388350	50.006551	5.757462	-6.665766	26.327695	-16.695794	4.566470	-136.737542	-3.362402	-3.472281	8.067414	-17.017648	17.0	↓	6	-6	→	6.0	17.0	14.0	Y	2	2	1	24	24-716352	716352	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	bottom	New York Yankees	NYY	Kansas City Royals	KC	2023-10-01	day	Clint Vondrak	0	False	212.0	field_out	Lineout	-16.4	5.5	3.6	18.0
50bd9d0f-eee5-4f99-9dc4-a1fa02594bf9	1	6	0	672580	R	Maikel Garcia	650633	R	Michael King	KC	NYY	118	147	Lineout	Maikel Garcia lines out to center fielder Este...	Lineout	{'homeRunBallparks': 0}	2	0	2	0	X	In Play	FF	4-Seam Fastball	In play, out(s)	X	hit_into_play	False	02	94.3	87.4	3.590000	1.730000	6.028961	0.396397	11.0	2377.0	-0.008739	3.769854	-2.256394	50.001334	5.865596	-6.578440	25.957664	-16.315596	7.339570	-137.357644	-2.731021	-3.389510	8.170515	-16.518106	17.0	↓	6	-6	→	5.0	16.0	14.0	Y	3	3	2	25	25-716352	716352	NaN	99.0	99.4	360	.410	18	0.0	114.37	-26.104127	54.75	358.29979	NaN	NaN	NaN	bottom	New York Yankees	NYY	Kansas City Royals	KC	2023-10-01	day	Clint Vondrak	0	False	203.0	field_out	Lineout	-15.8	4.9	3.6	16.8
6c79e8ff-4972-4ad1-85cb-f994727c1f90	1	7	0	677951	R	Bobby Witt Jr.	650633	R	Michael King	KC	NYY	118	147	Groundout	Bobby Witt Jr. grounds out, second baseman Os...	Groundout	{}	0	0	0	0	S	Strike	SI	Sinker	Called Strike	C	called_strike	False	00	93.5	87.0	3.403536	1.631027	5.979491	0.400484	9.0	1859.0	0.311409	1.618673	-2.256811	50.004739	5.486336	-17.570281	25.019013	-22.974243	10.189194	-135.885978	-6.196413	-9.236481	4.838141	-22.778260	23.0	↓	16	-16	→	15.0	23.0	7.0	Y	1	4	2	26	26-716352	716352	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	bottom	New York Yankees	NYY	Kansas City Royals	KC	2023-10-01	day	Clint Vondrak	1	False	165.0	field_out	Groundout	-23.2	15.0	6.0	33.6
e3f2d82a-9778-43aa-a813-05f91eb2122e	1	7	0	677951	R	Bobby Witt Jr.	650633	R	Michael King	KC	NYY	118	147	Groundout	Bobby Witt Jr. grounds out, second baseman Os...	Groundout	{}	1	0	1	0	B	Ball	SI	Sinker	Ball	B	ball	False	01	94.0	86.8	3.491020	1.660077	6.095591	0.398597	11.0	2321.0	-1.375257	2.676168	-2.402972	50.001801	5.610981	-15.254782	27.280516	-20.179332	5.599407	-136.873132	-4.246522	-7.957966	6.256626	-20.090125	20.0	↓	13	-13	→	14.0	20.0	11.0	Y	2	5	3	27	27-716352	716352	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	bottom	New York Yankees	NYY	Kansas City Royals	KC	2023-10-01	day	Clint Vondrak	1	False	215.0	field_out	Groundout	-19.9	13.4	4.8	33.6

Data cleaning

There are three major things we need to clean up about the data: (1) it includes the pitches that are swung that, not just the taken pitches that we care about; (2) it includes a lot of extra data in columns that we don't need; and (3) there are some rows with missing pitch tracking data.

Reorganize the columns

First, we rename some columns so that their names are more meaningful and so that they all follow the snake_case covnention (just for consistency's sake).

all_pitches.rename({'stand': 'batter_side',
                    'p_throws': 'pitcher_hand',
                    'pitch_type': 'pitch_code',
                    'pitch_name': 'pitch_description',
                    'description': 'result_description',
                    'plateTime': 'plate_time',
                    'zone': 'gameday_zone',
                    'pfxX': 'pfx_x', 'pfxZ': 'pfx_z',
                    'breakHorizontal': 'break_x', 'breakVertical': 'break_z',
                    'breakLength': 'break_length', 'breakAngle': 'break_angle',
                    "spinDirection": "spin_axis",
                    'runnerOn1B': 'runner_1b',
                    'runnerOn2B': 'runner_2b',
                    'runnerOn3B': 'runner_3b'}, axis=1,inplace=True)

Next, we'll extract just the columns we want. These columns include information about

• date/time of the game
• the teams playing
• the inning and number of outs
• if there are runners on base and if a runner is going on the pitch
• the pitcher and batter for that particular pitch
• the count (balls and strikes)
• the result of the pitch (e.g. ball, hit into play)
• the position of the ball as it crosses the front of home plate and MLB Gameday's zone determination
• the type of pitch (e.g. fastball, changeup)
• the speed of the pitch (both out of the hand and speed over home plate)
• kinematic information (position, velocity, acceleration) when the ball is 50 feet from the back of home plate
• spin on the ball based on pitcher's release
• break (how much movement the pitcher induces on the ball)
• eventual result of the plate appearance
• home plate umpire making the call

# reorder columns and drop the columns that we don't want
all_pitches = all_pitches[['game_pk', 'date', 'day_night',
                           'away_team', 'away_abbrev', 'home_team', 'home_abbrev',
                           'game_total_pitches',
                           'inning', 'half_inning', 'outs',
                           'runner_1b', 'runner_2b', 'runner_3b', 'runner_going',
                           'batter_name', 'batter_side', 'pitcher_name', 'pitcher_hand',
                           'pitch_number',
                           'balls', 'strikes',
                           'result_code', 'result_description',
                           'px', 'pz', 'sz_top', 'sz_bot',
                           'gameday_zone',
                           'pitch_code', 'pitch_description',
                           'start_speed', 'end_speed', 'plate_time',
                           'x0', 'y0', 'z0',
                           'vx0', 'vy0', 'vz0',
                           'ax', 'ay', 'az',
                           'pfx_x', 'pfx_z',
                           'spin_rate', 'spin_axis',
                           'break_x', 'break_z',
                           'break_length', 'break_angle',
                           'event_type', 'event_description',
                           'plate_umpire']]

Also, we have to update information about runners on base. It is reported as True if there is a runner on base and "NA" if there is not, which we will change to False.

all_pitches["runner_1b"] = all_pitches["runner_1b"].fillna(False)
all_pitches["runner_2b"] = all_pitches["runner_2b"].fillna(False)
all_pitches["runner_3b"] = all_pitches["runner_3b"].fillna(False)

Finally, here is the cleaned up data.

all_pitches.head()

	game_pk	date	day_night	away_team	away_abbrev	home_team	home_abbrev	game_total_pitches	inning	half_inning	outs	runner_1b	runner_2b	runner_3b	runner_going	batter_name	batter_side	pitcher_name	pitcher_hand	pitch_number	balls	strikes	result_code	result_description	px	pz	sz_top	sz_bot	gameday_zone	pitch_code	pitch_description	start_speed	end_speed	plate_time	x0	y0	z0	vx0	vy0	vz0	ax	ay	az	pfx_x	pfx_z	spin_rate	spin_axis	break_x	break_z	break_length	break_angle	event_type	event_description	plate_umpire
play_id
fd40dc91-e458-47d4-81d4-bdd654781440	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	23	1	bottom	0	False	False	False	False	Maikel Garcia	R	Michael King	R	1	0	0	C	Called Strike	-0.292692	2.207051	3.531020	1.612927	7.0	SI	Sinker	92.0	85.2	0.407594	-2.461166	50.003600	5.557445	8.973728	-133.710840	-4.062951	-17.086921	25.264212	-25.635070	-9.312735	3.563786	2491.0	200.0	15.2	-26.2	7.2	30.0	field_out	Lineout	Clint Vondrak
60d12f55-1c47-42da-8f3e-d3e2e6e47ee2	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	24	1	bottom	0	False	False	False	False	Maikel Garcia	R	Michael King	R	2	0	1	S	Swinging Strike	-1.158241	3.385914	3.590000	1.730000	11.0	FF	4-Seam Fastball	93.8	86.9	0.398518	-2.388350	50.006551	5.757462	4.566470	-136.737542	-3.362402	-6.665766	26.327695	-16.695794	-3.472281	8.067414	2330.0	212.0	5.5	-16.4	3.6	18.0	field_out	Lineout	Clint Vondrak
50bd9d0f-eee5-4f99-9dc4-a1fa02594bf9	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	25	1	bottom	0	False	False	False	False	Maikel Garcia	R	Michael King	R	3	0	2	X	In play, out(s)	-0.008739	3.769854	3.590000	1.730000	11.0	FF	4-Seam Fastball	94.3	87.4	0.396397	-2.256394	50.001334	5.865596	7.339570	-137.357644	-2.731021	-6.578440	25.957664	-16.315596	-3.389510	8.170515	2377.0	203.0	4.9	-15.8	3.6	16.8	field_out	Lineout	Clint Vondrak
6c79e8ff-4972-4ad1-85cb-f994727c1f90	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	26	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	1	0	0	C	Called Strike	0.311409	1.618673	3.403536	1.631027	9.0	SI	Sinker	93.5	87.0	0.400484	-2.256811	50.004739	5.486336	10.189194	-135.885978	-6.196413	-17.570281	25.019013	-22.974243	-9.236481	4.838141	1859.0	165.0	15.0	-23.2	6.0	33.6	field_out	Groundout	Clint Vondrak
e3f2d82a-9778-43aa-a813-05f91eb2122e	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	27	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	2	0	1	B	Ball	-1.375257	2.676168	3.491020	1.660077	11.0	SI	Sinker	94.0	86.8	0.398597	-2.402972	50.001801	5.610981	5.599407	-136.873132	-4.246522	-15.254782	27.280516	-20.179332	-7.957966	6.256626	2321.0	215.0	13.4	-19.9	4.8	33.6	field_out	Groundout	Clint Vondrak

Only including taken pitches

The dataset we have includes all pitches that have been thrown in MLB in 2023, whereas we only want the data of pitches that were taken (i.e. not swung at by the batter). To do this we look at the result_code column which contains a code corresponding to the result of a particular pitch.

The codes we are interested in are:

• *B (ball in dirt)
• B (ball)
• C (called strike)
• H (hit by pitch)
• I (intentional ball)
• P (pitchout)

For those who know a little about baseball you might find it unusual to include the hit by pitch as a call. However the rules of baseball stipulate that a batter is not awarded first base after being hit by a pitch if the pitch went through the strike zone. That makes a hit by pitch also implicitly a called ball, so we can verify if the hit by pitch was granted correctly. Unfortunately, we don't have data for hit by pitches not awarded because the pitch was judged to have gone through the strike zone. They are scored as ordinary called strikes.

result_codes = ["*B", "B", "C", "H", "I", "P"]
taken_pitches = all_pitches[all_pitches['result_code'].isin(result_codes)]
taken_pitches.head()

	game_pk	date	day_night	away_team	away_abbrev	home_team	home_abbrev	game_total_pitches	inning	half_inning	outs	runner_1b	runner_2b	runner_3b	runner_going	batter_name	batter_side	pitcher_name	pitcher_hand	pitch_number	balls	strikes	result_code	result_description	px	pz	sz_top	sz_bot	gameday_zone	pitch_code	pitch_description	start_speed	end_speed	plate_time	x0	y0	z0	vx0	vy0	vz0	ax	ay	az	pfx_x	pfx_z	spin_rate	spin_axis	break_x	break_z	break_length	break_angle	event_type	event_description	plate_umpire
play_id
fd40dc91-e458-47d4-81d4-bdd654781440	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	23	1	bottom	0	False	False	False	False	Maikel Garcia	R	Michael King	R	1	0	0	C	Called Strike	-0.292692	2.207051	3.531020	1.612927	7.0	SI	Sinker	92.0	85.2	0.407594	-2.461166	50.003600	5.557445	8.973728	-133.710840	-4.062951	-17.086921	25.264212	-25.635070	-9.312735	3.563786	2491.0	200.0	15.2	-26.2	7.2	30.0	field_out	Lineout	Clint Vondrak
6c79e8ff-4972-4ad1-85cb-f994727c1f90	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	26	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	1	0	0	C	Called Strike	0.311409	1.618673	3.403536	1.631027	9.0	SI	Sinker	93.5	87.0	0.400484	-2.256811	50.004739	5.486336	10.189194	-135.885978	-6.196413	-17.570281	25.019013	-22.974243	-9.236481	4.838141	1859.0	165.0	15.0	-23.2	6.0	33.6	field_out	Groundout	Clint Vondrak
e3f2d82a-9778-43aa-a813-05f91eb2122e	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	27	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	2	0	1	B	Ball	-1.375257	2.676168	3.491020	1.660077	11.0	SI	Sinker	94.0	86.8	0.398597	-2.402972	50.001801	5.610981	5.599407	-136.873132	-4.246522	-15.254782	27.280516	-20.179332	-7.957966	6.256626	2321.0	215.0	13.4	-19.9	4.8	33.6	field_out	Groundout	Clint Vondrak
38494e8c-a6db-48ae-93b0-08f09e346853	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	29	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	4	1	2	B	Ball	1.779492	1.317006	3.491020	1.718184	14.0	ST	Sweeper	81.9	76.2	0.458978	-2.404842	50.003641	5.380935	7.232091	-119.132844	-2.905202	12.379237	21.944713	-31.434472	8.574210	0.514236	2896.0	60.0	-17.3	-40.2	9.6	22.8	field_out	Groundout	Clint Vondrak
2334d79b-c2c7-4421-89b2-10cf4724d1d0	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	31	1	bottom	2	False	False	False	False	Salvador Perez	R	Michael King	R	1	0	0	C	Called Strike	0.448960	3.073323	3.540189	1.649124	3.0	SI	Sinker	93.9	87.2	0.398503	-2.280361	50.006529	5.488510	10.592485	-136.501232	-2.116903	-17.286584	24.924189	-24.112642	-8.994766	4.199174	2288.0	225.0	14.5	-23.3	6.0	32.4	strikeout	Strikeout	Clint Vondrak

Remove missing data

Sometimes, the dataset is missing information. We have already converted some expected missing data, where NA actually means False. However for the pitch location tracking sometimes we are just missing the parameters associated with a particular pitch. These seem to happen in either select games played at neutral site ballparks where the pitch tracking technology is not installed, or just random pitches from games where the technology is available. In both cases we assume that the fact that the data is missing is not related to the data itself, so we just remove those rows instead of doing any data imputation. In any case, the number of missing pitches is very small compared to the number of total pitches, so we do not expect the results of the analysis to change significantly had we had the full data from those pitches.

print("Number of taken pitches including incomplete observations:", len(taken_pitches))
taken_pitches = taken_pitches.dropna()
print("Number of taken pitches after removing incomplete observations:", len(taken_pitches))
taken_pitches.head()

Number of taken pitches including incomplete observations: 376681
Number of taken pitches after removing incomplete observations: 374426

	game_pk	date	day_night	away_team	away_abbrev	home_team	home_abbrev	game_total_pitches	inning	half_inning	outs	runner_1b	runner_2b	runner_3b	runner_going	batter_name	batter_side	pitcher_name	pitcher_hand	pitch_number	balls	strikes	result_code	result_description	px	pz	sz_top	sz_bot	gameday_zone	pitch_code	pitch_description	start_speed	end_speed	plate_time	x0	y0	z0	vx0	vy0	vz0	ax	ay	az	pfx_x	pfx_z	spin_rate	spin_axis	break_x	break_z	break_length	break_angle	event_type	event_description	plate_umpire
play_id
fd40dc91-e458-47d4-81d4-bdd654781440	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	23	1	bottom	0	False	False	False	False	Maikel Garcia	R	Michael King	R	1	0	0	C	Called Strike	-0.292692	2.207051	3.531020	1.612927	7.0	SI	Sinker	92.0	85.2	0.407594	-2.461166	50.003600	5.557445	8.973728	-133.710840	-4.062951	-17.086921	25.264212	-25.635070	-9.312735	3.563786	2491.0	200.0	15.2	-26.2	7.2	30.0	field_out	Lineout	Clint Vondrak
6c79e8ff-4972-4ad1-85cb-f994727c1f90	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	26	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	1	0	0	C	Called Strike	0.311409	1.618673	3.403536	1.631027	9.0	SI	Sinker	93.5	87.0	0.400484	-2.256811	50.004739	5.486336	10.189194	-135.885978	-6.196413	-17.570281	25.019013	-22.974243	-9.236481	4.838141	1859.0	165.0	15.0	-23.2	6.0	33.6	field_out	Groundout	Clint Vondrak
e3f2d82a-9778-43aa-a813-05f91eb2122e	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	27	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	2	0	1	B	Ball	-1.375257	2.676168	3.491020	1.660077	11.0	SI	Sinker	94.0	86.8	0.398597	-2.402972	50.001801	5.610981	5.599407	-136.873132	-4.246522	-15.254782	27.280516	-20.179332	-7.957966	6.256626	2321.0	215.0	13.4	-19.9	4.8	33.6	field_out	Groundout	Clint Vondrak
38494e8c-a6db-48ae-93b0-08f09e346853	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	29	1	bottom	1	False	False	False	False	Bobby Witt Jr.	R	Michael King	R	4	1	2	B	Ball	1.779492	1.317006	3.491020	1.718184	14.0	ST	Sweeper	81.9	76.2	0.458978	-2.404842	50.003641	5.380935	7.232091	-119.132844	-2.905202	12.379237	21.944713	-31.434472	8.574210	0.514236	2896.0	60.0	-17.3	-40.2	9.6	22.8	field_out	Groundout	Clint Vondrak
2334d79b-c2c7-4421-89b2-10cf4724d1d0	716352	2023-10-01	day	New York Yankees	NYY	Kansas City Royals	KC	31	1	bottom	2	False	False	False	False	Salvador Perez	R	Michael King	R	1	0	0	C	Called Strike	0.448960	3.073323	3.540189	1.649124	3.0	SI	Sinker	93.9	87.2	0.398503	-2.280361	50.006529	5.488510	10.592485	-136.501232	-2.116903	-17.286584	24.924189	-24.112642	-8.994766	4.199174	2288.0	225.0	14.5	-23.3	6.0	32.4	strikeout	Strikeout	Clint Vondrak

Compare the number of rows we had before (376,681) with the number of rows we have left (374,426), meaning that missing data represented about 0.6% of the total number of pitches.

Exploratory data analysis

We start by adding in a few utility columns that will make the analysis easier:

• expected_call encodes whether or not the ball entered the strike zone as a boolean value (True = strike, False = ball)
• actual_call represents what the umpire called it (True = strike, False = ball)
• correct_call determines whether or not the umpire's call was correct

def expected_strike(zone):
    return int(zone) < 10

def actual_strike(result_code):
    return result_code == "C"

taken_pitches['expected_call'] = taken_pitches['gameday_zone'].apply(expected_strike)
taken_pitches['actual_call']   = taken_pitches['result_code'].apply(actual_strike)
taken_pitches['correct_call']  = taken_pitches['expected_call'] == taken_pitches['actual_call']

Overall umpire performance in 2023

We begin the analysis by getting a sense of the scale of how many calls umpires make in a season and per game.

print("Number of pitches thrown in 2023:", len(all_pitches))
print("Average pitches thrown per game in 2023:", len(all_pitches) / 2430)
print("Number of taken pitches in 2023:", len(taken_pitches))
print("Average taken pitches per game in 2023:", len(taken_pitches) / 2430)
print("Percent of all pitches taken in 2023:", len(taken_pitches) / len(all_pitches) * 100)

Number of pitches thrown in 2023: 717945
Average pitches thrown per game in 2023: 295.45061728395063
Number of taken pitches in 2023: 374426
Average taken pitches per game in 2023: 154.08477366255144
Percent of all pitches taken in 2023: 52.15246293239733

One of the surprising takeaways from this data is how many pitches umpires look at where they don't have to make a call, ball or strike. Nearly half of the pitches thrown in MLB in 2023 are swung at. This reduces the workload of umpires having to make those ball and strike calls (although this becomes workload managing other aspects of the game).

Now, let's see how they have done at all these pitches.

print("Number of incorrect calls in 2023:", len(taken_pitches[taken_pitches["correct_call"] == False]))
print("Average incorrect calls per game in 2023:", len(taken_pitches[taken_pitches["correct_call"] == False])/ 2430)
overall_accuracy = taken_pitches["correct_call"].mean() * 100
print("Overall umpire accuracy in 2023:", overall_accuracy)
print("Overall bad call ratio (BCR) in 2023:", 100 - (taken_pitches["correct_call"].mean() * 100))

Number of incorrect calls in 2023: 26741
Average incorrect calls per game in 2023: 11.004526748971193
Overall umpire accuracy in 2023: 92.85813485174641
Overall bad call ratio (BCR) in 2023: 7.141865148253586

This shows that over the course of a season, umpires have missed a staggering number of calls, about 7% of all ball/strike calls they make are wrong, and over 10 per game. This proportion of the number of incorrect calls is known as the bad call ratio (BCR), and is already a well-studied topics in umpire sabermetrics.

It may seem like umpires are terrible at their jobs! Although this tutorial does not cover historical data, we can tell you based on a 2019 Boston University study that overall umpire accuracy has increased year on year for over a decade, and that 2023 was the best year in terms of umpire accuracy. Although you may still say that this is still not enough!

Accuracy by pitch speed

Pitchers often vary the speed of pitches in order to confuse a batter's timing. In addition, pitchers whose fastballs are very fast (say, at least 100 mph) often dominate hitters because of the limited time that they have to react to an oncoming pitch. We would like to review how umpires stack up against pitches of different speed. Note that pitch speed is typically considered "out-of-hand" i.e. when the balls is released from the pitcher's hand (baseballs usually slow down as it travels towards home plate).

First, let's see a distribution of the speeds of all taken pitches in 2023:

plt.hist(all_pitches["start_speed"], bins=np.arange(75, 101, 1))
plt.ylabel("Count of pitches in 2023")
plt.xlabel("Release speed of pitch (mph)")
plt.title("Histogram of pitch release speeds of taken pitches in 2023")
plt.show()

Most pitches fall between 75 and 100 mph. Notably, there's a bimodal distribution present here. This is because of different pitch types: the first peak encompasses off-speed pitches and breaking balls, while the second peak covers fastballs. We'll discuss this in greater detail in the next section. For now, let's look at umpire accuracy as a function of pitch speed:

taken_pitches["speed"] = pd.cut(taken_pitches["start_speed"], bins=np.arange(75, 101, 1))
speed_pitches = taken_pitches.groupby("speed", observed=False)
plt.plot(np.arange(76, 101, 1), speed_pitches["correct_call"].mean() * 100)
plt.plot([75, 100], [overall_accuracy, overall_accuracy], linestyle='dashed')
plt.xlabel("Release speed of pitch (mph)")
plt.ylabel("Umpire accuracy on called pitches")
plt.title("Umpire accuracy vs. pitch speed")
plt.show()

Recall that the average accuracy between all pitches is about 92.8%, which we have also graphed as a dashed orange line. Compared to the overall average, umpires seem to be much more accurate for pitches less than 90 mph, while umpires have more trouble with pitches between 90 and 100 mph, although the accuracy seems to recover nearer to 100 mph. This could be explainable with the claim that slow pitches are easier to track with the eyes versus faster pitches. But is having a pitch be merely faster more difficult to call? We think there is more going on.

Accuracy by pitch type

As we may have spoiled earlier, not all pitches are created equal. Pitches not only vary in their speed, but also the spin rate as thrown by the pitcher. The spin has a tendency to influence the break of the pitch, which is how much the pitch moves left or right, up or down (accounting for gravity). For example, the curveball is a type of pitch, with a downward spin which gives the appearance that the ball is diving towards the plate as it moves towards the batter.

MLB's Statcast defines three classes of pitches: fastballs, the main type of pitch thrown the hardest; offspeed pitches, designed to look like fastballs, but are thrown slower in order to disrupt the batter's timing and prompt a swing and miss; and breaking balls, thrown with a lot of spin to invoke significant horziontal or vertical break.

The pitch types we will cover are the following (specifying both the two letter pitch_code as appears in the data and the full name of the pitch)

• fastballs
  • FF (four-seam fastball)
  • SI (sinking fastball)
  • FC (cut fastball)
• offspeed pitches
  • CH (changeup)
  • FS (splitter)
• breaking balls
  • CU (curveball)
  • KC (knuckle curve)
  • SL (slider)
  • ST (sweeper)
  • SV (slurve)

There are a few other pitch types, but we exclude them since there were fewer than 1,000 calls made on that type of pitch in 2023:

pitch_types = pd.DataFrame({
                        'name': pitch_code,
                        'num_calls': pitches['correct_call'].count(),
                        'accuracy': pitches['correct_call'].mean() * 100,
                    } for pitch_code, pitches in taken_pitches.groupby("pitch_code"))
pitch_types = pitch_types[pitch_types["num_calls"] > 1000].sort_values(by="num_calls", ascending=False)

plt.bar(pitch_types['name'], pitch_types['num_calls'],
        color=['red', 'green', 'red', 'blue', 'green', 'red', 'green', 'blue', 'green', 'green'])
plt.xlabel("Pitch type")
plt.ylabel("Number of calls")
plt.title("Number of calls by pitch type")
plt.plot()

[]

We've colored the bars so that fastballs are in red, breaking balls are in green, and offspeed pitches in blue.

Now, let's see how accurate MLB umpires are against these type of pitches:

pitch_types = pd.DataFrame({
                        'name': pitch_code,
                        'num_calls': pitches['correct_call'].count(),
                        'accuracy': pitches['correct_call'].mean() * 100,
                    } for pitch_code, pitches in taken_pitches.groupby("pitch_code"))
pitch_types = pitch_types[pitch_types["num_calls"] > 1000].sort_values(by="accuracy", ascending=False)

plt.bar(pitch_types['name'], pitch_types['accuracy'],
        color=['blue', 'blue', 'green', 'green', 'green', 'green', 'green', 'red', 'red', 'red'])
plt.plot([-0.5, 9.5], [overall_accuracy, overall_accuracy], linestyle='dashed', color='orange')
plt.ylim(90, 96)
plt.xlabel("Pitch type")
plt.ylabel("Umpire accuracy on called pitches")
plt.title("Umpire accuracy vs. pitch type")
plt.plot()

[]

We've included the overall accuracy as a dashed orange line. As it turns out, accuracy is correlated to pitch type: fastballs are the hardest to call, followed by breaking balls, and offspeed pitches are the easiest with over 95% accuracy.

Heatmaps of called strikes

As we explained earlier, the (computerized) strike zone is a 2D rectangle, so we'd like to see how accurate umpires are in certain locations of the strike zone.

Before we can do this, however, we should normalize the px and pz values for the pitch location. Here's how we'll do it:

• The horizontal px location will be normalized depending on the batter's handedness, which is in batter_side. This is because horizontal pitches are considered in terms of "inside" and "outside" to the batter rather than left and right. In fact, umpires tend to set up on the inside part of the plate of the batter:

  

  The normalized norm_px value will be on the same scale as px, except that negative values of px always correspond to the inside part of the plate while positive values are to the outside part of the plate, instead of merely left and right.

• The verticality of the pitch depends on pz and the bounds of the vertical strike zone sz_top and sz_bot, so we fix a standard SZ_TOP and SZ_BOT corresponding to the average among all batters, which is roughly 3.40 and 1.60, respectively.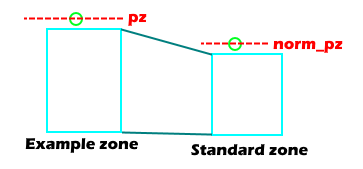

  

  The norm_pz value records the vertical position of the pitch with respect to SZ_TOP and SZ_BOT.

SZ_TOP = 3.40
SZ_BOT = 1.60
RAD = 0.12

def normalized_pz(df):
    pz = df['pz']
    sz_top = df['sz_top']
    sz_bot = df['sz_bot']

    if pz > sz_top - RAD:
        return pz - sz_top + SZ_TOP
    elif pz < sz_bot + RAD:
        return pz - sz_bot + SZ_BOT
    else:
        return SZ_BOT + (SZ_TOP - SZ_BOT) * ((pz - sz_bot) / (sz_top - sz_bot))

def normalized_px(df):
    pz = df['px']
    side = df['batter_side']

    return -pz if side == "L" else pz

taken_pitches["px_norm"] = taken_pitches.apply(normalized_px, axis=1)
taken_pitches["pz_norm"] = taken_pitches.apply(normalized_pz, axis=1)

Now that we have these normalized values, we can now graph all pitches from 2023 on the same strike zone. We'll do this by constructing a heatmap of called strikes.

PLATE_EDGE = 17/24 + 0.12
MIDDLE = (3.4 + 1.6) / 2
HALF_HEIGHT = 1.02

taken_pitches["horiz_zone"] = pd.cut(taken_pitches["px_norm"], bins=np.linspace(-PLATE_EDGE * 2, PLATE_EDGE * 2, 33))
taken_pitches["vert_zone"]  = pd.cut(taken_pitches["pz_norm"], bins=np.linspace(MIDDLE - HALF_HEIGHT * 2, MIDDLE + HALF_HEIGHT * 2, 33))

zoned_pitches = taken_pitches.groupby(["vert_zone", "horiz_zone"], observed=False)["expected_call"].mean().unstack()[::-1]
sns.heatmap(zoned_pitches)

plt.gca().set_aspect(0.255/0.207)       # set square aspect ratio
plt.plot([8,8,24,24,8],[8,24,24,8,8], color="green")
plt.xticks([], [])
plt.xlabel("Normalized horizontal location")
plt.yticks([], [])
plt.ylabel("Normalized vertical location")
plt.title("Heatmap of expected calls on pitches")
plt.show()

zoned_pitches = taken_pitches.groupby(["vert_zone", "horiz_zone"], observed=False)["actual_call"].mean().unstack()[::-1]
sns.heatmap(zoned_pitches)

plt.gca().set_aspect(0.255/0.207)       # set square aspect ratio
plt.plot([8,8,24,24,8],[8,24,24,8,8], color="green")
plt.xticks([], [])
plt.xlabel("Normalized horizontal location")
plt.yticks([], [])
plt.ylabel("Normalized vertical location")
plt.title("Heatmap of expected calls on pitches")
plt.show()

The first heatmap shows what the ideal heatmap should look like. We have set up the scale so that any pitch within the green box is in the zone, and thus should have been called a strike (and so should be completely bright white). Any pitch outside the box should be called a ball (and so should be completely black).

Each square in the second heatmap represents the proportion of pitches which are in that area that were called strikes by MLB umpires in 2023. What we see is that the zone is not necessarily a rectangle, but more an oval. It shows that the pitches at the corners are not called strikes very often, while pitches off the inside and outside edges of the zone are called strikes at a pretty high proportion. In particular, we can see that the area off to the right side (which denotes the outside zone) is slightly brighter than on the left side (which is the inside zone).

This shows that umpires are more likely to call a strike off the outside part of the plate compare to the inside part. This theory lines up with how umpires typically set up to the inside of the batter. Since they are looking straight on at that edge, they end up having an easier time calling pitches to the inside part, rather than the outside part, where they are looking off at an angle.

Umpires less likely to strike out batters

As we have discussed earlier, the call of an umpire can have a significant influence on the result of a plate appearance. For example, an incorrect strike call on two strikes means that the batter is out, rather than having more changes to bat. The heatmap above showed us how often umpires called strikes in certain places of the zone. Let's see how it looks when an umpire makes a call when the count has two strikes.

zoned_pitches_strike2 = taken_pitches[taken_pitches["strikes"] == 2].groupby(["vert_zone", "horiz_zone"], observed=False)["actual_call"].mean().unstack()[::-1]
sns.heatmap(zoned_pitches_strike2)

plt.gca().set_aspect(0.255/0.207)       # set square aspect ratio
plt.plot([8,8,24,24,8],[8,24,24,8,8], color="green")
plt.xticks([], [])
plt.xlabel("Normalized horizontal location")
plt.yticks([], [])
plt.ylabel("Normalized vertical location")
plt.title("Heatmap of expected calls on pitches with 2 strikes")
plt.show()

lim = (zoned_pitches_strike2 - zoned_pitches).abs().max().max()
sns.heatmap(zoned_pitches_strike2 - zoned_pitches, cmap="coolwarm", vmin=-lim, vmax=lim)

plt.gca().set_aspect(0.255/0.207)       # set square aspect ratio
plt.plot([8,8,24,24,8],[8,24,24,8,8], color="green")
plt.xticks([], [])
plt.xlabel("Normalized horizontal location")
plt.yticks([], [])
plt.ylabel("Normalized vertical location")
plt.title("Difference of expected calls on pitches with 2 strikes")
plt.show()

The first heatmap seemed hard to interpret, so we have a second chart which plots the difference from the heatmap on two strikes versus the heatmap for all pitches. Red squares mean that umpires are more likely to call a strike on with two strikes in the count than in general, and blue squares the opposite. The overwhelming blue on the chart shows us that umpires are much less to call strike 3 on a batter, especially on pitches on the edge of the zone.

Analysis, hypothesis testing, & ML

We would like to build a model which represents the average umpire based on 2023 data. This would help us get a better sense of who the better umpires are and what aspects of a pitch are more influential towards ball and strike calls. This involves creating a binary classifier using pitch data to predict what an umpire's call would be. Note that we don't care about what the expected call of a pitch is (representing whether or not the pitch was in the zone or not), since that is very easy to calculate. Instead, we want to predict what the umpire's actual call will be. We will use the decision tree classifier to accomplish this.

First, we must define the subset of features from the data that we will use to train the model. We have selected the following features based on our previous discussions:

• px_norm: horizontal position of the pitch taking batter's handedness into account
• pz: vertical location of the pitch
• sz_top and sz_bot: vertical bounds for the strike zone. Note that we aren't using pz_norm, since the bounds of the strike zones themselves can have influence on the pitch call
• break_x and break_z: this encodes the amount of break of the pitch, which is a function of the pitch type discussed earlier
• start_speed: release speed of the pitch
• balls and strikes: the current count

feature_cols = ['px_norm', 'pz', 'sz_top', 'sz_bot', 'break_x', 'break_z', 'start_speed', 'balls', 'strikes']
X = taken_pitches[feature_cols] # Features
y = taken_pitches.actual_call

Next, we split up the data into training data and test data. Since there is a large amount of data available (370,000 pitches), we choose a split of 80% training data, 20% test data.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, shuffle=True)

print("Training set size:", len(X_train))
print("Testing set size:", len(X_test))

Training set size: 299540
Testing set size: 74886

We now set up our decision tree classifier and train it using the training data that we found.

tree_model = DecisionTreeClassifier()
tree_model = tree_model.fit(X_train, y_train)

With our model fitted to the training data, we now use it to predict the classification of the test data.

y_pred_tree = tree_model.predict(X_test)

Let's see how accurate this was!

print("Accuracy: ", metrics.accuracy_score(y_test, y_pred_tree))

Accuracy:  0.9090751275271747

This is not a bad score. It's not possible to get a perfect score outside of the training data because it's possible (and likely happened) that two umpires have called the same exact pitch two different ways.

Let's get a classification report for this.

print(classification_report(y_test, y_pred_tree))

              precision    recall  f1-score   support

       False       0.93      0.93      0.93     51445
        True       0.85      0.85      0.85     23441

    accuracy                           0.91     74886
   macro avg       0.89      0.89      0.89     74886
weighted avg       0.91      0.91      0.91     74886

We construct a confusion matrix corresponding to the results of predicting the test data.

class_names=["False", "True"] # name  of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
cnf_matrix_tree = metrics.confusion_matrix(y_test, y_pred_tree)
sns.heatmap(pd.DataFrame(cnf_matrix_tree), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')

Text(0.5, 427.9555555555555, 'Predicted label')

We also plot the receiver operating characteristic curve:

y_pred_proba_tree = tree_model.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test,  y_pred_proba_tree)
auc = metrics.roc_auc_score(y_test, y_pred_proba_tree)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.title("Receiver operating characteristics curve")
plt.show()

And here's a look into the inner workings of the decision tree.

plt.figure(figsize=(20,10))
tree.plot_tree(tree_model, filled=True, fontsize=10, feature_names=feature_cols, max_depth=3)
plt.show()

Last, we'd like to look at how important all the features are in predicting the output.

# Checking feature importance
importances = pd.DataFrame({'feature': X_train[feature_cols].columns, 'importance': tree_model.feature_importances_}).sort_values('importance', ascending=False)
print(importances)

       feature  importance
0      px_norm    0.444101
1           pz    0.397211
2       sz_top    0.035773
3       sz_bot    0.035729
4      break_x    0.027359
5      break_z    0.024478
6  start_speed    0.023337
7        balls    0.006391
8      strikes    0.005621

Unsurprisingly, the vertical and horizontal positions pz and px_norm are the most important features towards determining if an umpire will call a pitch a ball or a strike. Next up is sz_bot and sz_top, which we would expect because it is needed to determine if a pitch falls inthe vertical strike zone.

By the computer rules, those would be the only four factors that determine ball or strike. However, we also see importance in break_x, break_z, and start_speed, showing that the shape of the pitch also has some influence on the pitch's call. We also see that the count of balls and strikes are the least important features.

Insight and policy decisions

At the end of the day, we would like to reward good MLB umpires and recognize superior ability in calling balls and strikes. In practice, this is done through crew chief promotions (becoming the leader of the four-man umpiring crew he is a part of) and postseason assignments (where he will get to work the most important games).

We would also like to highlight struggling umpires and determine what they need to spend time improving.

As an example, we'll use our trained model to assess the performance of umpires during the 2023 postseason (we only considered regular season up to this point, but postseason gives us a little more data that we can apply our models to). First, let's get the data from those games.

r = requests.get("https://statsapi.mlb.com/api/v1/schedule",
                 params={"sportId": 1,              # indicates Major League Baseball (AL + NL)
                         "startDate": "2023-01-01", # start of 2023
                         "endDate": "2023-12-01",   # end of 2023
                         "gameTypes": ["F", "D", "L", "W"]})
# postseason game types include
#   F = wild card series
#   D = divison series
#   L = league championship series
#   W = world series

# The query includes a list of dates, and each date has a list of games for that day.
query = json.loads(r.content)

# extract each game_pk
game_pks = []
for date in query['dates']:
    for game in date['games']:
        game_pks.append(game['gamePk'])

# get rid of duplicates (happens due to postponements, which double counts the game for the originally scheduled date and actual date of the game)
games = list(set(game_pks))

print(len(games))                               # total number of games

41

game_pitches = list(map(get_game_pitches, games))

postseason_pitches = pd.concat(game_pitches, ignore_index = True)
postseason_pitches.set_index("play_id", inplace=True)
postseason_pitches.head()

	inning	ab_number	cap_index	batter	stand	batter_name	pitcher	p_throws	pitcher_name	team_batting	team_fielding	team_batting_id	team_fielding_id	result	des	events	contextMetrics	strikes	balls	pre_strikes	pre_balls	call	call_name	pitch_type	pitch_name	description	result_code	pitch_call	is_strike_swinging	balls_and_strikes	start_speed	end_speed	sz_top	sz_bot	extension	plateTime	zone	spin_rate	px	pz	x0	y0	z0	ax	ay	az	vx0	vy0	vz0	pfxX	pfxZ	pfxZWithGravity	pfxZWithGravityNice	pfxZDirection	pfxXWithGravity	pfxXNoAbs	pfxXDirection	breakX	breakZ	inducedBreakZ	hit_speed_round	hit_speed	hit_distance	xba	hit_angle	is_barrel	hc_x	hc_x_ft	hc_y	hc_y_ft	is_bip_out	pitch_number	player_total_pitches	player_total_pitches_pitch_types	game_total_pitches	rowId	game_pk	player_name	runnerOn1B	runnerOn2B	runnerOn3B	half_inning	away_team	away_abbrev	home_team	home_abbrev	date	day_night	plate_umpire	outs	runner_going	spinDirection	event_type	event_description	breakVertical	breakHorizontal	breakLength	breakAngle
play_id
4a069011-5958-4fc4-af7c-1a8e37395891	1	4	0	606466	R	Ketel Marte	650911	L	Cristopher Sánchez	AZ	PHI	109	143	Groundout	Ketel Marte grounds out, second baseman Bryson...	Groundout	{'homeRunBallparks': 0}	0	0	0	0	X	In Play	SI	Sinker	In play, out(s)	X	hit_into_play	False	00	92.2	84.4	3.540000	1.690000	6.791236	0.408719	9	1970	0.807688	2.162640	1.748492	50.002941	5.834315	19.856549	29.578406	-26.116662	-6.241417	-134.122073	-4.777216	10.922046	3.330782	-26.611854	27	↓	18	18	←	18.0	27.0	6.0	100.0	99.6	6	.110	-22	0.0	138.08	31.045509	124.83	189.381761	Y	1	1	1	23	23-748544	748544	PHI	NaN	NaN	NaN	bottom	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	2023-10-20	night	Mike Muchlinski	0	False	117.0	field_out	Groundout	-27.1	-18.4	7.2	34.8
1c820466-a1e0-4c76-a43f-798929e1a444	1	5	0	682998	L	Corbin Carroll	650911	L	Cristopher Sánchez	AZ	PHI	109	143	Groundout	Corbin Carroll grounds out, pitcher Cristopher...	Groundout	{}	0	0	0	0	S	Strike	SI	Sinker	Called Strike	C	called_strike	False	00	92.9	85.1	3.170675	1.576307	7.080770	0.405783	4	2015	-0.554020	2.560673	1.719392	50.004482	5.804752	19.404949	28.987894	-24.830040	-9.698387	-134.912303	-3.986018	10.511402	3.978887	-25.055092	25	↓	18	18	←	17.0	25.0	7.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	Y	1	2	2	24	24-748544	748544	NaN	NaN	NaN	NaN	bottom	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	2023-10-20	night	Mike Muchlinski	1	False	115.0	field_out	Groundout	-25.2	-17.0	7.2	33.6
c1a0cdf7-d190-4be0-964c-bd4de540240e	1	5	0	682998	L	Corbin Carroll	650911	L	Cristopher Sánchez	AZ	PHI	109	143	Groundout	Corbin Carroll grounds out, pitcher Cristopher...	Groundout	{}	1	0	1	0	S	Strike	SI	Sinker	Foul	F	foul	False	01	92.8	85.1	3.140000	1.480000	7.046580	0.406061	5	1934	-0.090677	2.041874	1.807166	50.001698	5.771773	18.373196	29.081882	-25.919565	-8.503464	-134.844971	-5.066663	9.968781	3.392270	-26.089912	26	↓	17	17	←	16.0	26.0	6.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	Y	2	3	3	25	25-748544	748544	NaN	NaN	NaN	NaN	bottom	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	2023-10-20	night	Mike Muchlinski	1	False	111.0	field_out	Groundout	-26.6	-16.2	7.2	31.2
cd48ca82-50a3-4603-a9fa-8a8cbce8944e	1	5	0	682998	L	Corbin Carroll	650911	L	Cristopher Sánchez	AZ	PHI	109	143	Groundout	Corbin Carroll grounds out, pitcher Cristopher...	Groundout	{}	2	0	2	0	B	Ball	CH	Changeup	Ball	B	ball	False	02	82.9	76.4	3.170675	1.477469	7.000006	0.455212	14	1953	0.113231	0.314335	1.933014	50.001007	5.593012	13.870536	23.808931	-31.199647	-7.242118	-120.413762	-5.970624	9.464740	0.660322	-38.877095	39	↓	16	16	←	15.0	39.0	1.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	Y	3	4	1	26	26-748544	748544	NaN	NaN	NaN	NaN	bottom	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	2023-10-20	night	Mike Muchlinski	1	False	98.0	field_out	Groundout	-40.1	-15.4	9.6	21.6
3c3f127a-a0e8-46bb-903e-9b8a0afbbca6	1	5	0	682998	L	Corbin Carroll	650911	L	Cristopher Sánchez	AZ	PHI	109	143	Groundout	Corbin Carroll grounds out, pitcher Cristopher...	Groundout	{'homeRunBallparks': 0}	2	1	2	1	X	In Play	CH	Changeup	In play, out(s)	X	hit_into_play	False	12	83.2	76.4	3.140000	1.480000	6.907456	0.452515	12	1933	1.045599	2.659124	1.871132	50.003868	5.889874	14.959764	23.784962	-33.967735	-5.102493	-121.073603	-0.612647	10.082693	-1.208386	-41.562701	42	↓	17	17	←	17.0	41.0	-1.0	61.0	60.8	19	.070	-7	0.0	125.30	0.241108	180.76	54.570326	Y	4	5	2	27	27-748544	748544	NaN	NaN	NaN	NaN	bottom	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	2023-10-20	night	Mike Muchlinski	1	False	97.0	field_out	Groundout	-41.6	-17.0	9.6	22.8

Next, we'll clean this dataset in the same way we cleaned the regular season pitches and add in some extra columns that we added in the exploratory data analysis section.

postseason_pitches.rename({'stand': 'batter_side',
                    'p_throws': 'pitcher_hand',
                    'pitch_type': 'pitch_code',
                    'pitch_name': 'pitch_description',
                    'description': 'result_description',
                    'plateTime': 'plate_time',
                    'zone': 'gameday_zone',
                    'pfxX': 'pfx_x', 'pfxZ': 'pfx_z',
                    'breakHorizontal': 'break_x', 'breakVertical': 'break_z',
                    'breakLength': 'break_length', 'breakAngle': 'break_angle',
                    "spinDirection": "spin_axis",
                    'runnerOn1B': 'runner_1b',
                    'runnerOn2B': 'runner_2b',
                    'runnerOn3B': 'runner_3b'}, axis=1,inplace=True)
# reorder columns and drop the columns that we don't want
postseason_pitches = postseason_pitches[['game_pk', 'date', 'day_night',
                           'away_team', 'away_abbrev', 'home_team', 'home_abbrev',
                           'game_total_pitches',
                           'inning', 'half_inning', 'outs',
                           'runner_1b', 'runner_2b', 'runner_3b', 'runner_going',
                           'batter_name', 'batter_side', 'pitcher_name', 'pitcher_hand',
                           'pitch_number',
                           'balls', 'strikes',
                           'result_code', 'result_description',
                           'px', 'pz', 'sz_top', 'sz_bot',
                           'gameday_zone',
                           'pitch_code', 'pitch_description',
                           'start_speed', 'end_speed', 'plate_time',
                           'x0', 'y0', 'z0',
                           'vx0', 'vy0', 'vz0',
                           'ax', 'ay', 'az',
                           'pfx_x', 'pfx_z',
                           'spin_rate', 'spin_axis',
                           'break_x', 'break_z',
                           'break_length', 'break_angle',
                           'event_type', 'event_description',
                           'plate_umpire']]
postseason_pitches["runner_1b"] = postseason_pitches["runner_1b"].fillna(False)
postseason_pitches["runner_2b"] = postseason_pitches["runner_2b"].fillna(False)
postseason_pitches["runner_3b"] = postseason_pitches["runner_3b"].fillna(False)
result_codes = ["*B", "B", "C", "H", "I", "P"]
postseason_taken_pitches = postseason_pitches[postseason_pitches['result_code'].isin(result_codes)]
postseason_taken_pitches = postseason_taken_pitches.dropna()

postseason_taken_pitches['expected_call'] = postseason_taken_pitches['gameday_zone'].apply(expected_strike)
postseason_taken_pitches['actual_call']   = postseason_taken_pitches['result_code'].apply(actual_strike)
postseason_taken_pitches['correct_call']  = postseason_taken_pitches['expected_call'] == postseason_taken_pitches['actual_call']

postseason_taken_pitches["px_norm"] = postseason_taken_pitches.apply(normalized_px, axis=1)
postseason_taken_pitches["pz_norm"] = postseason_taken_pitches.apply(normalized_pz, axis=1)

print("Number of taken pitches in the 2023 postseason:", len(postseason_pitches))
postseason_taken_pitches.head()

Number of taken pitches in the 2023 postseason: 11829

	game_pk	date	day_night	away_team	away_abbrev	home_team	home_abbrev	game_total_pitches	inning	half_inning	outs	runner_1b	runner_2b	runner_3b	runner_going	batter_name	batter_side	pitcher_name	pitcher_hand	pitch_number	balls	strikes	result_code	result_description	px	pz	sz_top	sz_bot	gameday_zone	pitch_code	pitch_description	start_speed	end_speed	plate_time	x0	y0	z0	vx0	vy0	vz0	ax	ay	az	pfx_x	pfx_z	spin_rate	spin_axis	break_x	break_z	break_length	break_angle	event_type	event_description	plate_umpire	expected_call	actual_call	correct_call	px_norm	pz_norm
play_id
1c820466-a1e0-4c76-a43f-798929e1a444	748544	2023-10-20	night	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	24	1	bottom	1	False	False	False	False	Corbin Carroll	L	Cristopher Sánchez	L	1	0	0	C	Called Strike	-0.554020	2.560673	3.170675	1.576307	4	SI	Sinker	92.9	85.1	0.405783	1.719392	50.004482	5.804752	-9.698387	-134.912303	-3.986018	19.404949	28.987894	-24.830040	10.511402	3.978887	2015	115.0	-17.0	-25.2	7.2	33.6	field_out	Groundout	Mike Muchlinski	True	True	True	0.554020	2.711324
cd48ca82-50a3-4603-a9fa-8a8cbce8944e	748544	2023-10-20	night	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	26	1	bottom	1	False	False	False	False	Corbin Carroll	L	Cristopher Sánchez	L	3	0	2	B	Ball	0.113231	0.314335	3.170675	1.477469	14	CH	Changeup	82.9	76.4	0.455212	1.933014	50.001007	5.593012	-7.242118	-120.413762	-5.970624	13.870536	23.808931	-31.199647	9.464740	0.660322	1953	98.0	-15.4	-40.1	9.6	21.6	field_out	Groundout	Mike Muchlinski	False	False	True	-0.113231	0.436866
388feb8e-d1f5-4d21-9e13-4a352304b64e	748544	2023-10-20	night	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	28	1	bottom	2	False	False	False	False	Gabriel Moreno	R	Cristopher Sánchez	L	1	0	0	C	Called Strike	0.721545	2.922909	3.387163	1.540415	3	SI	Sinker	92.9	85.2	0.404773	1.715875	50.003105	5.898742	-6.095500	-135.249815	-3.287519	18.377603	29.130897	-24.914057	9.906351	3.914399	1905	112.0	-16.7	-25.1	7.2	33.6	field_out	Pop Out	Mike Muchlinski	True	True	True	0.721545	2.947498
d9cb9575-854d-4a0e-ad6f-cdb9fb9a9015	748544	2023-10-20	night	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	29	1	bottom	2	False	False	False	False	Gabriel Moreno	R	Cristopher Sánchez	L	2	0	1	B	Ball	1.675490	2.123989	3.387163	1.540415	14	CH	Changeup	83.4	76.7	0.451117	1.973322	50.000187	5.693863	-3.682712	-121.498678	-1.472341	14.231832	24.210927	-33.958942	9.538274	-1.200168	1931	96.0	-16.3	-41.5	9.6	21.6	field_out	Pop Out	Mike Muchlinski	False	False	True	1.675490	2.168802
217c2826-97bd-4c58-b897-7ba41b98b6ed	748544	2023-10-20	night	Philadelphia Phillies	PHI	Arizona Diamondbacks	AZ	30	1	bottom	2	False	False	False	False	Gabriel Moreno	R	Cristopher Sánchez	L	3	1	1	B	Ball	1.806079	2.216680	3.387163	1.540415	14	CH	Changeup	82.8	76.2	0.454571	1.968776	50.004734	5.781904	-3.459456	-120.521864	-1.592752	14.618907	23.557022	-32.770355	9.942277	-0.402354	1845	98.0	-17.2	-40.8	9.6	22.8	field_out	Pop Out	Mike Muchlinski	False	False	True	1.806079	2.259146

Next, we will apply our model by calculating a "credit" value for each pitch:

• if the umpire's actual call is the same as the predicted call by the model, then the credit for that pitch is 0, since that umpire and the average umpire both agree (so one can't be more correct than the other)
• if the umpire's actual call is different than the predicted call, and the umpire's call was correct and the predicated call was wrong, then the umpire recieves +1 credit for that pitch for getting the call correct compared to an average umpire
• if the umpire's actual call is different than the predicted call, and the umpire's call was wrong and the predicated call was correct, then the umpire recieves -1 credit for that pitch for getting the call wrong compared to the average umpire

postseason_taken_pitches["pred_call"] = tree_model.predict(postseason_taken_pitches[feature_cols])
def credit(pitch):
    if pitch["pred_call"] == pitch["actual_call"]:
        return 0
    else:
        if pitch['pred_call'] == pitch['expected_call']:
            return -1
        else:
            return 1
postseason_taken_pitches["credit"] = postseason_taken_pitches.apply(credit, axis=1)

Now that we have this, we can group together the umpires in the test set, and calculate the umpire's accuracy and the sum of all the credits, which we will name correct calls above average.

umpire_stats = pd.DataFrame({
                        'umpire_name': umpire,
                        'called': len(pitches),
                        'num_inc': len(pitches[pitches['correct_call'] == False]),
                        'accuracy': pitches['correct_call'].mean(),
                        'calls_above_avg': pitches['credit'].sum()
                    } for umpire, pitches in postseason_taken_pitches.groupby("plate_umpire"))
umpire_stats.set_index("umpire_name", inplace=True)

Here are the five most accurate umpires that we found:

umpire_stats.sort_values("accuracy", ascending=False).head(5)

	called	num_inc	accuracy	calls_above_avg
umpire_name
Lance Barksdale	129	2	0.984496	6
Todd Tichenor	134	4	0.970149	0
Bill Miller	158	7	0.955696	5
Brian O'Nora	133	6	0.954887	3
Brian Knight	296	14	0.952703	15

And here are the five least accurate umpires:

umpire_stats.sort_values("accuracy", ascending=True).head(5)

	called	num_inc	accuracy	calls_above_avg
umpire_name
Doug Eddings	280	31	0.889286	-10
Marvin Hudson	145	16	0.889655	-2
Jansen Visconti	131	14	0.893130	-3
Dan Iassogna	137	14	0.897810	-11
David Rackley	292	27	0.907534	-13

Lastly, we will use our new correct calls above average metric to determine which umpires are doing better with respect to his fellow umpires:

umpire_stats.sort_values("calls_above_avg", ascending=False).head(5)

	called	num_inc	accuracy	calls_above_avg
umpire_name
Brian Knight	296	14	0.952703	15
Mark Ripperger	337	19	0.943620	8
Tripp Gibson	287	17	0.940767	7
Lance Barksdale	129	2	0.984496	6
Bill Miller	158	7	0.955696	5

And here are the five worst umpires by that metric.

umpire_stats.sort_values("calls_above_avg", ascending=True).head(5)

	called	num_inc	accuracy	calls_above_avg
umpire_name
David Rackley	292	27	0.907534	-13
Dan Iassogna	137	14	0.897810	-11
Doug Eddings	280	31	0.889286	-10
Andy Fletcher	282	24	0.914894	-7
Dan Bellino	329	25	0.924012	-6

We plot these two metrics together in a scatterplot to show that there is a positive correlation between accuracy and correct calls above average with a linear regression.

plt.scatter(umpire_stats["accuracy"], umpire_stats["calls_above_avg"])


reg = linear_model.LinearRegression()
reg.fit(umpire_stats["accuracy"].values.reshape(-1, 1), umpire_stats["calls_above_avg"])

def regression(x):
    return reg.coef_[0] * x + reg.intercept_

# plot the regression line
plt.axline((0.875, regression(0.875)), (1, regression(1)))

plt.title("Correct calls above average vs. accuracy")
plt.xlabel("Accuracy")
plt.ylabel("Correct calls above average")
plt.show()

The issue with strict metrics like accuracy is that they tend to be agnostic to the type of miss. That is, a borderline miss is treated as much of a missed call as a huge miss. The correct calls above accuracy is just one metric which hopes to shed more light on who the better (and worse) umpires are. If an umpire has a low accuracy number, but a high number of correct calls above average number, then we can surmise that the umpire had a more difficult set of pitches to call which is why they were in accurate. But in comparison to how an average umpire would call it, he was still pretty good. The linear regression gives us that border between being better than the accuracy number suggests: if an umpire is above the trendline, then we can see he did a better job than the raw accuracy number suggested, while umpires below the line did worse than expected.

We used the model trained on 2023 regular season data to assess performance of umpires in the 2023 postseason, which may not be the most ideal conditions since the goal of the model is to find who the best umpires are that deserve postseason assignments. In the future, one could use the 2023 regular season model to assess umpires from the 2024 regular season, and reward the best umpires of 2024 with postseason assignments.